5.5 More Complex Turtle Graphs
Simple instructions, when combined with looping, can produce quite complex patterns. Consider the following process (with results shown in Figure 5.13):
turtle_init(1000, 1000, mode = "clip")
turtle_do({
turtle_setpos(600,400)
turtle_right(90)
for (i in 1:2000) {
turtle_right(i)
turtle_forward(sqrt(i))
}
})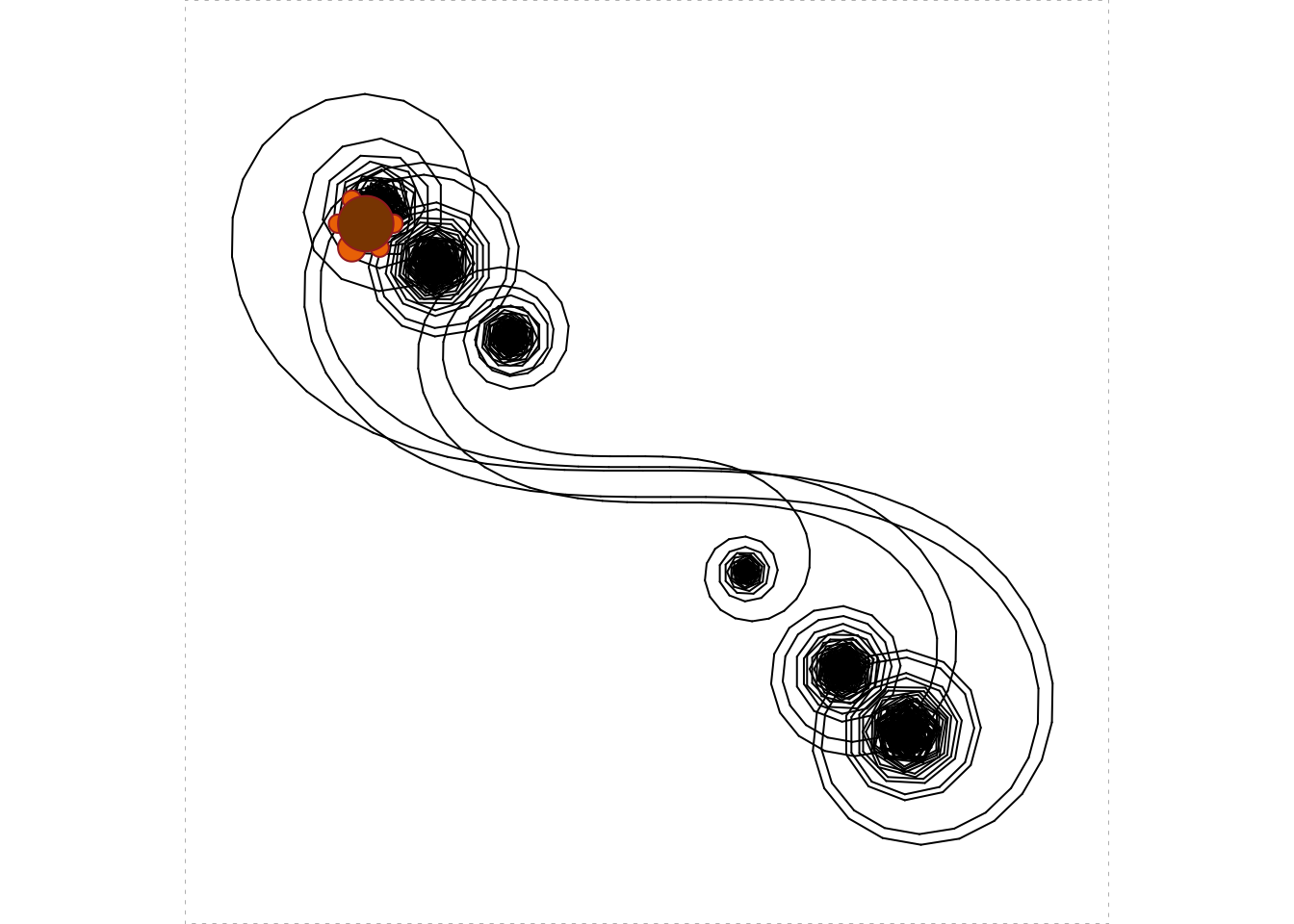
Figure 5.13: Galactic Zany!
You might enjoy figuring out why this pattern occurs. As you ponder this, it might help to construct a set of “ragged” spirals with somewhat larger steps, and pause at each step. Code like the following might be useful:16
turtle_init(1000, 1000, mode = "clip")
turtle_do({
i <- 1
turtle_right(90)
repeat {
bidding <- readline("Proceed? (Enter q to quit) ")
if ( bidding == "q") break
turtle_right(i)
turtle_forward(2*sqrt(i))
cat(paste0("Turned ", i, " degrees,\n"))
cat(paste0("stepped forward ", round(2*sqrt(i), 3), " units.\n"))
cat("Turtle's current angle is: ", turtle_getangle(), " degrees.\n")
i <- i + 20
}
cat("All done!")
})Also don’t forget that every 360 degrees is a full turn around the circle, so when the turtle’s angle is, say 720 degrees, it’s the same as an angle of 360 degrees which is the same as an angle of 0 degrees. All three angles amount to the same direction.↩︎