Exercises

Write a function called turtle_gon() that draws a regular polygon. The user should be able to specify the side-length and the number of sides. Start with turtle_init() and use your function to draw a regular dodecagon (twelve sides) with each side having a side length of 15 units. Your figure should not stray outside of the turtle’s field, so you may have to adjust the position of your turtle a bit prior to calling your function.
Write a function called turtle_star() that can make stars like the ones in Figure 5.17. Here are the required parameters:
- n: the number of rays in a star (default should be 6);
- length: the length of the rays (default should be 20);
- color: the color of the rays (default should be "red");
- type: the line-type of the rays (default should be 1);
- width: the line-width of the rays (default should be 1).
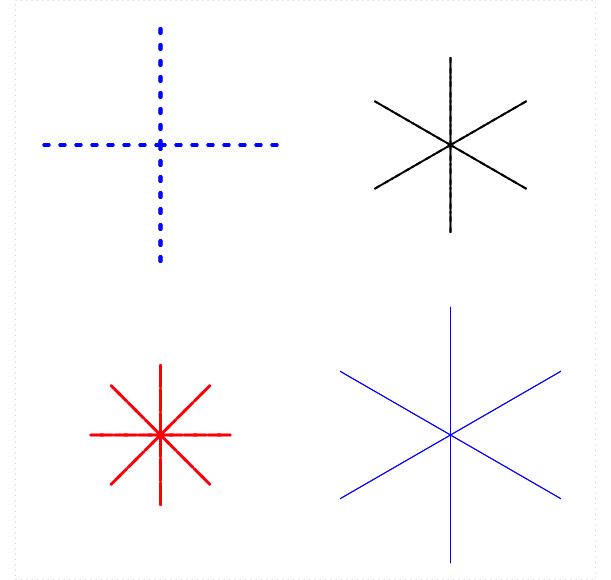
Figure 5.17: Sample Stars

Starting with turtle_init(), use your function to create a star with 10 rays, each of length 20 units. The lines should be red and dashed. I’ll leave the thickness up to you.
Make a new star function turtle_rstar() in which the lengths of the rays are not determined by the user but instead vary randomly from 5 to 25 units, as in Figure 5.18: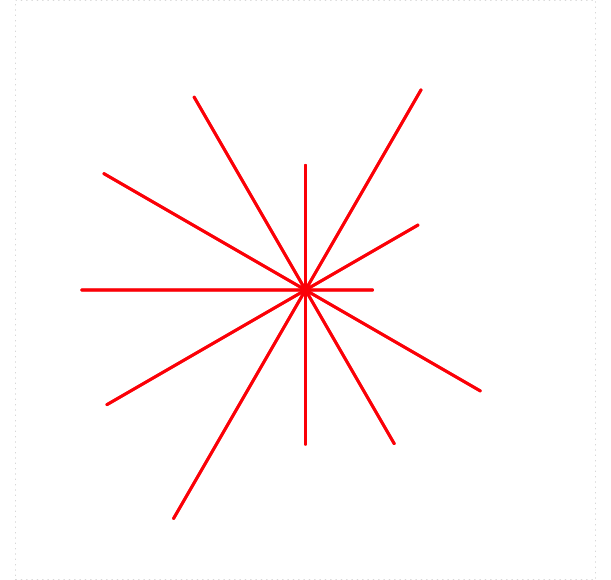

Figure 5.18: A star with rays of random lengths.

There is no longer a legnth parameter, but the names and default-values for the other parameters should be the same as in the previous exercise. Starting from turtle_init(50,50) make a random star with 20 rays and a line-thickness of 3. Other parameters should be left at their default-values.

Hint: You’ll probably use a loop to draw each ray of the star. As you go through the loop, get a random ray-length using the runif() function:
```
randomLength <- runif(1, min = 5, max = 25)
```
Then have the turtle make the ray by moving forward and backward by that amount.
Make a new star function turtle_rstarColors() that behaves like turtle_rstar() except that instead of being determined by the user the ray-color varies randomly from one ray to another, as in Figure 5.19:

Figure 5.19: A star with rays of random lengths and random colors.

Each ray should have a color drawn randomly from the vector of all colors given by colors(). Starting from turtle_init(50,50) make a random star with 20 rays and a line-thickness of 6. Other parameters should be left at their default-values.

Hint: You’ll probably use a loop to draw each ray of the star. As you go through the loop, get a new random color like this:
```
randomColor <- sample(colors(), size = 1)
```
Then set the turtle’s color accordingly:
```
turtle_col(col = randomColor)
```
(*) Our turtle_quick_pollack() function has successive strokes attached to each other. However, Jackson Pollack famous “drip” style involved placing brush-strokes at seemingly random locations on the canvas—successive strokes weren’t placed together. Modify our Pollack-painter function so that each new stroke appears as a random location inside the canvas. If you really get into it, research colors in R and try to come up with your own scheme for randomizing colors.