5 Turtle Graphics
In this chapter we will practice our knowledge of R—and of basic programming concepts—in the context of a special R-package for graphics: package TurtleGraphics (Cena et al. 2018). Many of the examples from this Chapter are drawn from the Vignette for the package.1
5.1 Basic Movements
First, we begin by loading the package:
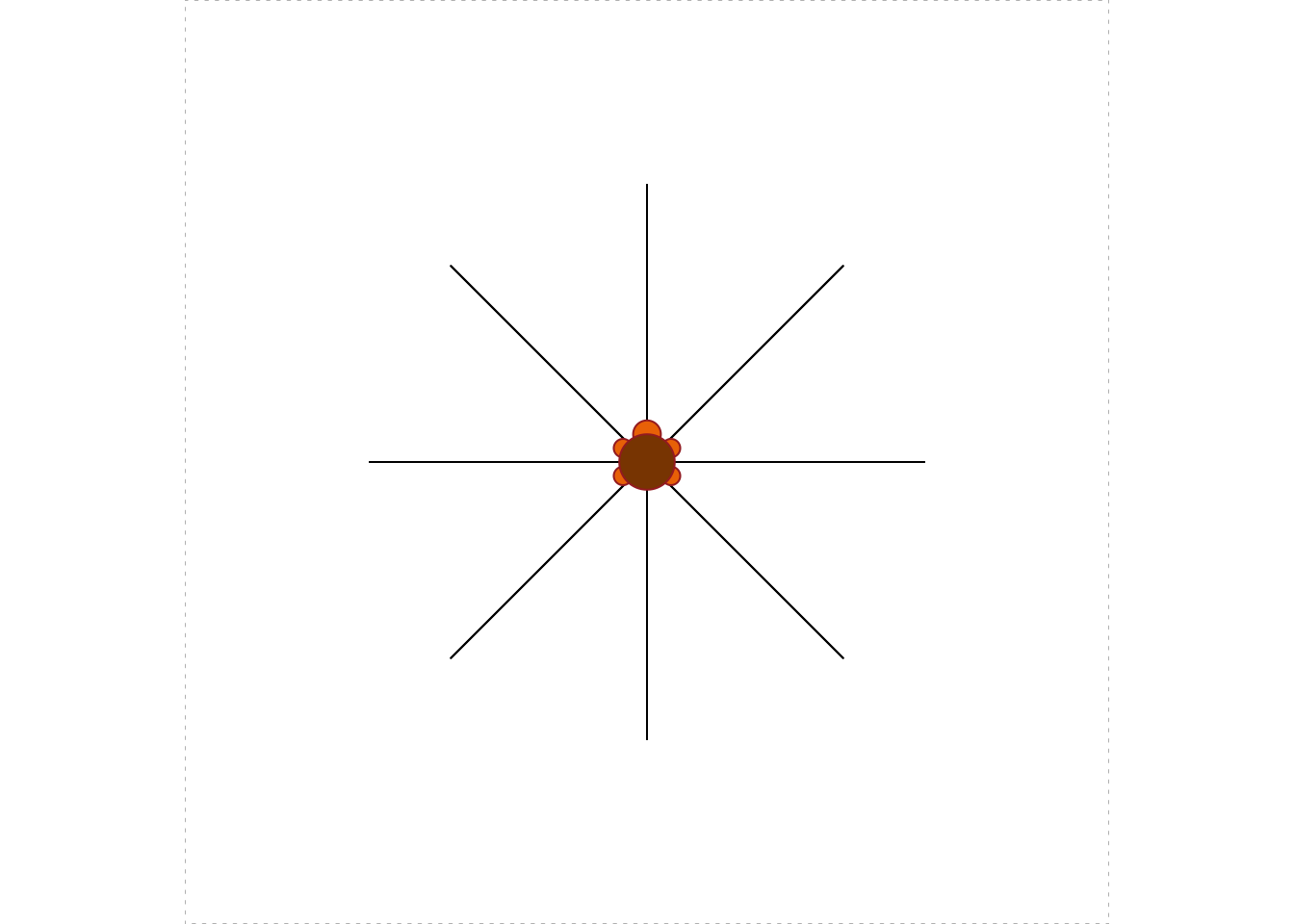
library(TurtleGraphics)In order to create a Turtle Graphics scenario, call the function turtle_init(). You get the plot shown in Figure 5.1.
turtle_init()
By default the turtle is positioned in the middle of a square of dimensions 100 units by 100 units. (These dimensions can be changed, as we will see later on.)
You can get the turtle’s position at any time:
turtle_getpos()x y
50 50 The turtle also begins facing North. This is considered to be angle 0, as you can tell by asking for the current angle of the turtle:
turtle_getangle()angle
0 Now let’s make the turtle move. If you are following along on your own computer, it’s best to run the lines of code one at a time, so you can see the effect of each command. (If you run multiples lines, you’ll only see the graph produced by the final line.)
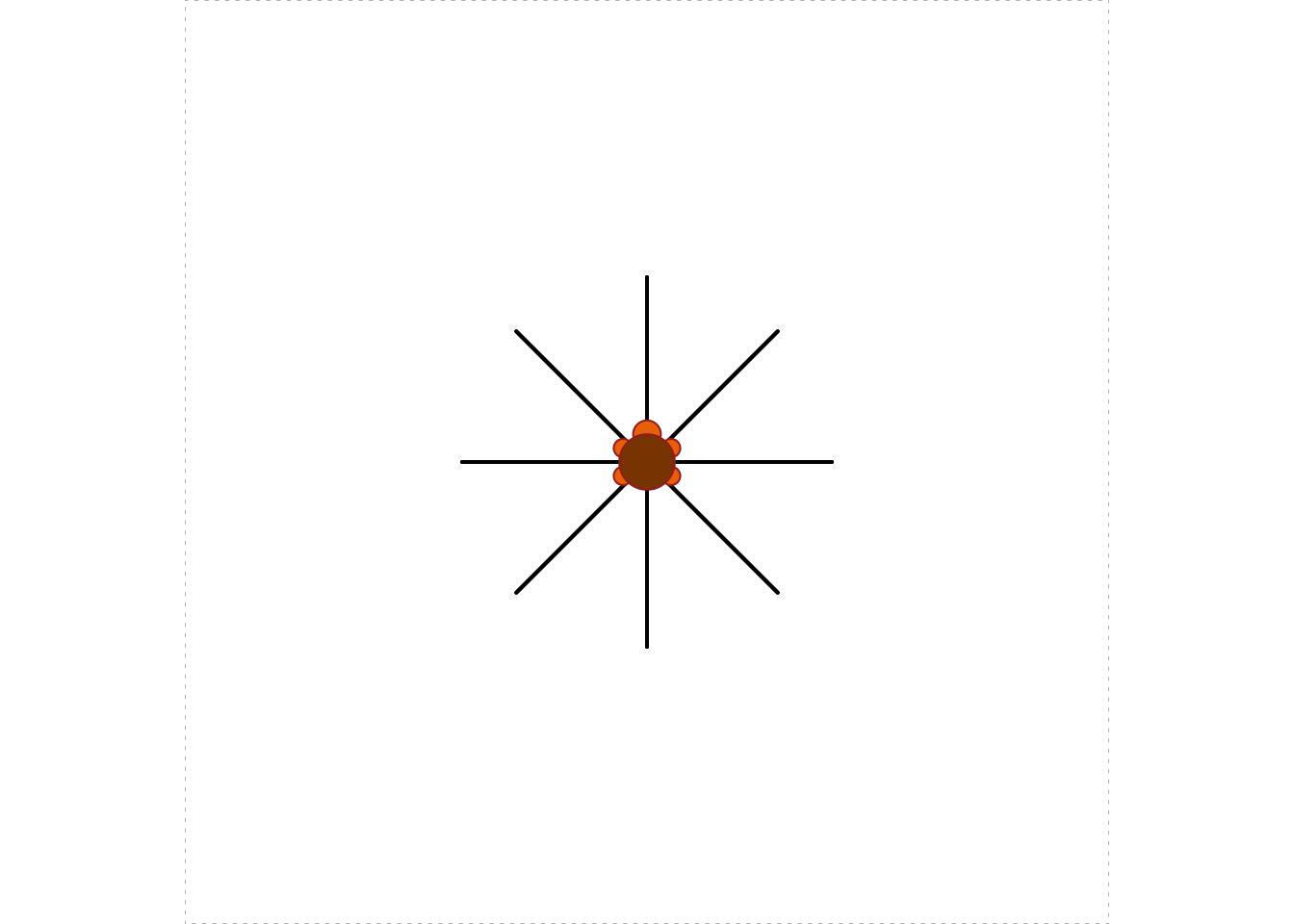
turtle_forward(dist = 30)
turtle_backward(dist = 10)
The result appears in Figure 5.2. Next we’ll add a little triangle:
turtle_right(90)
turtle_forward(10)
turtle_left(angle = 135)
turtle_forward(14.14)
turtle_left(angle = 90)
turtle_forward(14.14)
turtle_left(angle = 135)
turtle_forward(10)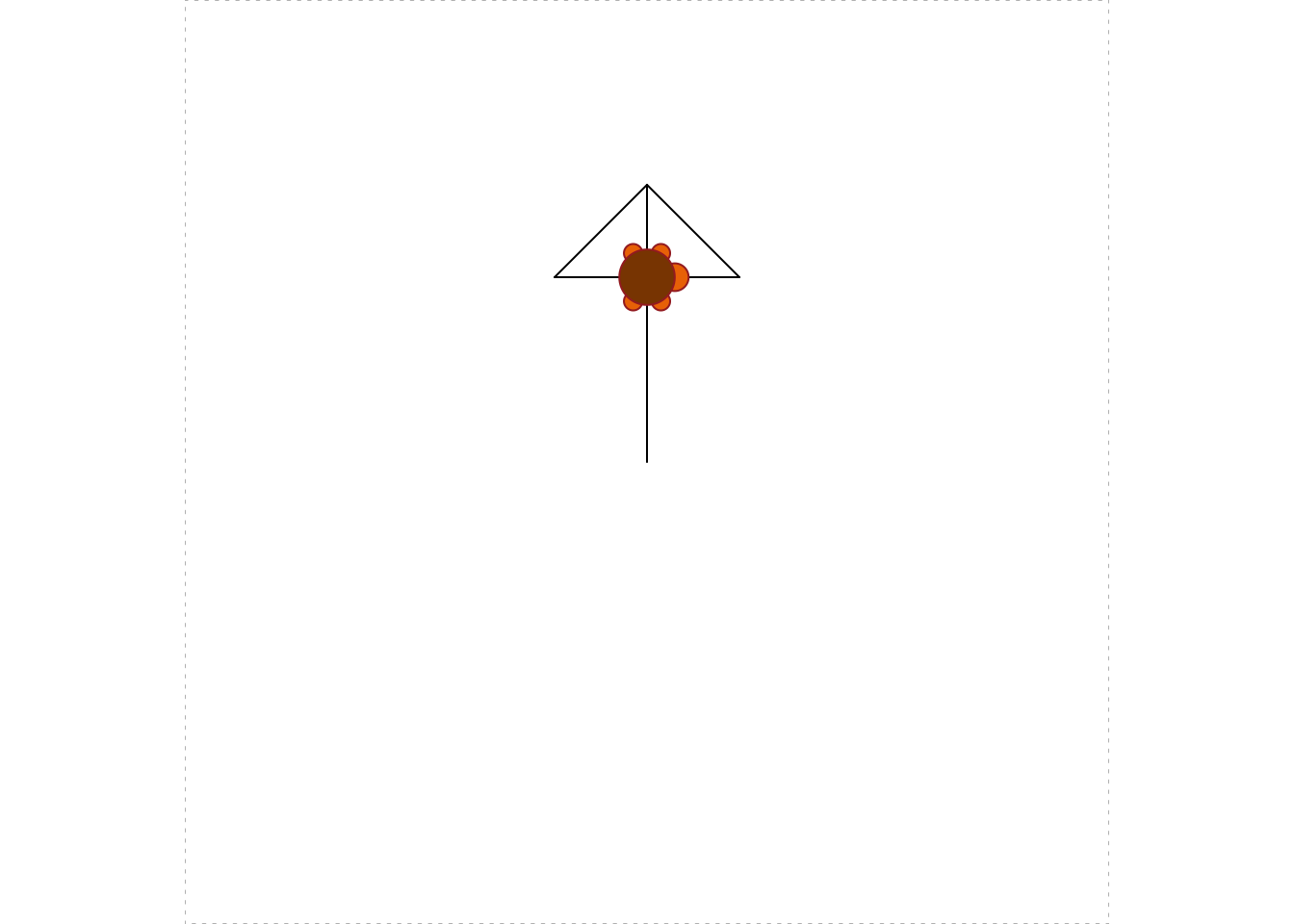
You can see the triangle in Figure 5.3.
The turtle is set in the “down” position, so that it leaves a trace out the path that it follows. You can avoid the trace by pulling the turtle “up” with turtle_up(). Whenever you want to restore the tracing, call turtle_down(). See Figure 5.4 for the results of the following code.
turtle_up() # stop tracing
turtle_right(angle = 90)
turtle_forward(dist = 10)
turtle_right(angle = 90)
turtle_forward(dist = 17)
turtle_down() # start tracing again
turtle_left(angle = 180)
turtle_forward(dist = 34)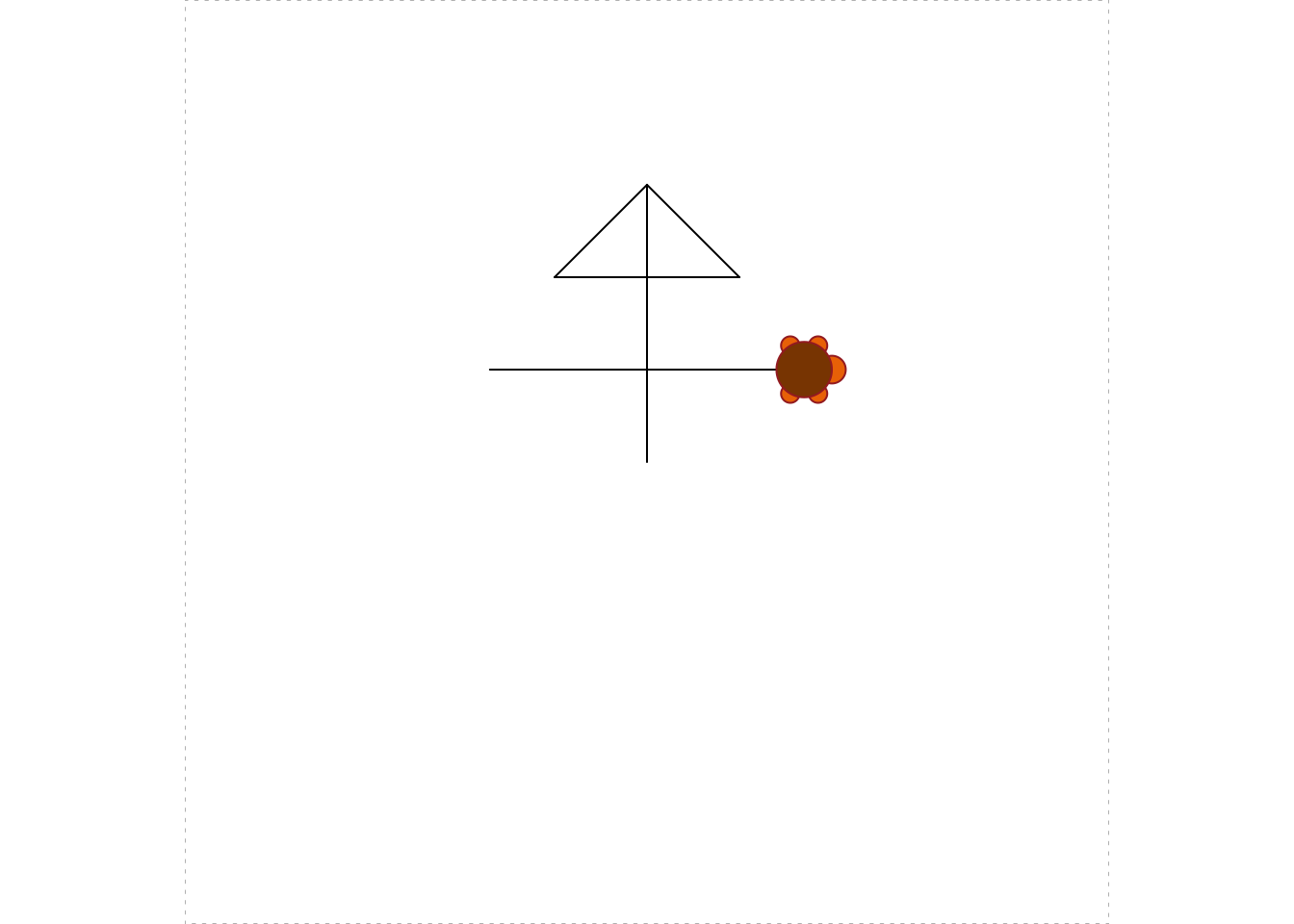
You can change the color of the lines your turtle draws:
turtle_col(col = "green")In R here are many, many colors to choose from, and 657 of them even have names. To view them, use the colors() function:
colors()You can also hide your turtle, and show it again any time you like. See Figure 5.5 for the results of the following code.
turtle_hide()
turtle_left(angle = 150)
turtle_forward(dist = 20)
turtle_left(angle = 60)
turtle_forward(dist = 20)
turtle_show()
Finally, you can choose the type of line your turtle draws, and the width of the line. See Figure 5.6 for the results of the following code.
turtle_left(angle = 150)
turtle_lty(lty = 4)
turtle_forward(dist = 17)
turtle_lwd(lwd = 3)
turtle_forward(dist = 15)
Note: you can learn more about lty and lwd with help(par).
5.2 Making Many Movements: An Introduction to Looping
Eventually we want to make some complex figures that require many movements on the part of the turtle. In order to make these go faster, we can turn off some of the turtle graphing by wrapping the desired movements in turtle_do(). See Figure 5.7 for the results of the following code.
turtle_init()
turtle_do({
turtle_move(10)
turtle_turn(45)
turtle_move(15)
})
(turtle_turn() turns to the left by default.)
Of course, for such a small number of movements using turtle_do() does not matter much, but we will practice using it for a bit.
How might we make a square? The following code offers one way to do it. See Figure 5.8 for the results.
turtle_init()
turtle_do({
turtle_move(20)
turtle_right(90)
turtle_move(20)
turtle_right(90)
turtle_move(20)
turtle_right(90)
turtle_move(20)
turtle_right(90)
})
This is a bit repetitious. Surely we can take advantage of the fact that there is a clear pattern to the turtle’s movements. A for-loop seems called for, as in the following code to build the square:
turtle_init()
turtle_do({
for(i in 1:4) {
turtle_forward(dist = 20)
turtle_right(angle = 90)
}
})As we learned in Chapter 4, the more you need to repeat a particular pattern, the more it makes sense to write your code with a loop. Suppose, for example, that you decide to make regular octagons. A regular octagon has eight sides, and you turn 45 degrees after drawing each side. You can do this easily by modifying the square-code as follows (see Figure 5.9 for the results):
turtle_init()
turtle_do({
for(i in 1:8) {
turtle_forward(dist = 20)
turtle_right(angle = 45)
}
})
You can even make many small turns, so that the resulting figure starts to look like a circle (see Figure 5.10 for the results):
turtle_init()
turtle_setpos(x = 30, y = 50)
turtle_do({
for(i in 1:180) {
turtle_forward(dist = 1)
turtle_right(angle = 2)
}
})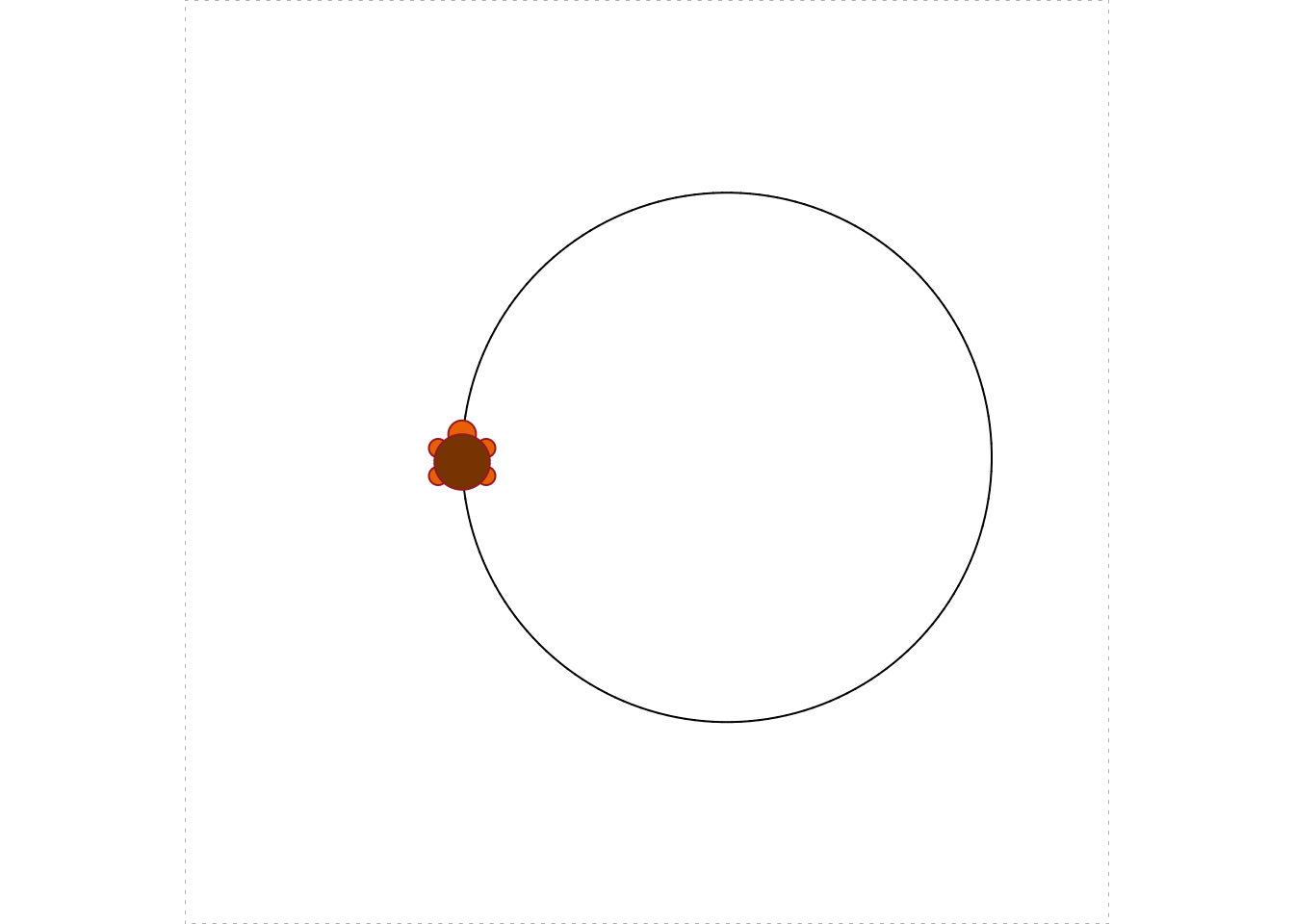
Notice that in the above code the turtle was initially set a bit to the left of center, so that the resulting circle would be situated close to middle of the region.
If you allow the index variable to be involved in the computations in the body of the loop then you can start making more complex figures. For example, here is the code for a spiral (see Figure 5.11 for the results):
turtle_init(width = 150, height = 150, mode = "clip")
turtle_do({
turtle_right(90)
for (i in 1:720) {
turtle_left(1)
turtle_forward(i/720)
}
})
The turtle turns one degree every time R goes through the loop, but the amount it travels forward (\(i/720\)) increases as the index variable i increases.
Another thing to notice is that we set the width and height of the region ourselves, so that the spiral would fit into it. We also set mode to clip rather then leaving it at its default value of error. With mode = "clip", R won’t throw an error message at you when the turtle moves outside of its region. Clip-mode is very handy when you are developing a graph and don’t know in advance precisely where the turtle will go.
5.2.1 Practice Exercises
Note: Code-fields in this textbook don’t work well with functions from TurtleGraphics, so you should work these exercises in R Studio.
5.3 Writing Turtle Functions
Once you have designed some shapes that you think you might want to draw again, you should write them up as functions. Here for example, is the code for a function that makes squares:
turtle_square <- function(side) {
turtle_do({
for (i in 1:4) {
turtle_forward(side)
turtle_right(90)
}
})
}Note that the user can vary the length of a side. You would use it like this:
turtle_init(mode = "clip")
turtle_square(side = 30)5.3.1 Practice Exercises
Note: Code-fields in this textbook don’t work well with functions from TurtleGraphics, so you should work these exercises in R Studio.
5.4 Random Moves
So far our turtle has moved in very regular and disciplined ways. It’s time to break the pattern, a bit. R has a quite a few functions to generate numbers that look “random”; we will use some of these functions to make the turtle move about randomly.
5.4.1 Sampling from a Vector
You have already met the sample() function (see Section 4.2.1). Let’s take a closer look at it.
sample() makes a random choice from a given vector. From the R-help we read that the general form of a call to sample is as follows:
sample(x, size, replace = FALSE, prob = NULL)In the above call:
xis the vector from which we wish to sample (R refers to it as the “population”);sizeis the number of random samples we want;replacesays whether or not to replace each member of the population after we have sampled it.probspecifies the desired probability for each member of the population to be chosen. If it is left at its default value ofNULL, then each element of the vector has the same chance to be chosen.
A few examples will help us understand how the arguments work:
vec <- 1:10 # we'll sample from this vector
sample(vec, 1)[1] 7We got only one number because we set size to 1. Every element in vec had an equal chance of being the element selected. This time we got 7, but if you were to run the function again for yourself your results would probably be different.
Let’s sample 10 numbers from vec:
sample(vec, 10) [1] 1 9 10 5 4 3 2 7 8 6Because replace was left at its default value of FALSE, R did not replace numbers after pulling them from the vec. After each sample, the remaining numbers all had the same chance to be picked next. Setting size to the length of x and keeping replace = FALSE therefore has the effect of randomly shuffling the elements of x.
Of course when replace = FALSE any attempt to sample more than the number of elements of vec will result in an error:
sample(vec, 11)Error in sample.int(length(x), size, replace, prob): cannot take a sample larger than the population when 'replace = FALSE'When we set replace = TRUE then each selected element is returned to the population. At any stage, the chance for a given member of the population to be the one selected next is the same—no matter how many times that member has already been selected. Thus, when replace = TRUE you are liable to see repeats:
sample(vec, 20, replace = TRUE) [1] 5 3 5 5 8 8 9 10 5 9 4 5 6 4 10 7 1 8 3 5When the prob parameter is left at its NULL value, R gives each member of the population the same chance to be the member that is selected. It is possible to adjust the probabilities of selection by setting prob to a vector of probabilities (one for each corresponding member of x). Thus, suppose we want to select 20 numbers from vec, according to the following the probabilities:
- 5% chance of selection, for each number from 1 to 8;
- 30% chance for 9 to be selected;
- 30% chance for 10 to be selected.
Then we can call sample() like this:
sample(
vec, 20,
replace = TRUE,
prob = c(rep(0.05, 8), 0.30, 0.30)
) [1] 9 1 9 10 9 6 8 9 4 7 10 10 9 2 6 9 5 9 10 10Notice the majority of 9’s and 10’s: this was fairly likely to occur since each selection had a 60% chance of turning out to be 9 or 10.
5.4.2 Application: a Bouncing Turtle
Let’s apply sample() to design a scenario in which the turtle moves a fixed amount at each step, but the direction—north, east, south, or west—is completely random. When the turtle reaches the boundary of its domain, however, we would like it to “bounce back”: i.e., take a step in the direction opposite to the step that brought it to the boundary. We will also query the user prior to each step, asking if he/she wants to see another move. This not only allows the user to decide when to end the scenario; it also permits the user to see where the turtle is after each step.
One possible implementation is as follows:
turtle_bounce <- function(side = 60, step= 10) {
if ( (side/2) %% step != 0 ) {
stop("Side-length divided by two must be a multiple of step.")
}
bounds <- c(0, side)
turtle_init(side, side, mode = "clip")
origin <- turtle_getpos()
cp <- turtle_getpos()
repeat {
move <- readline(prompt = "Go Again? (enter q to quit): ")
if ( move == "q") break
x <- cp["x"]
y <- cp["y"]
if (x %in% bounds | y %in% bounds) {
angle <- 180
} else {
angle <- sample(c(0,90,180,270), 1)
}
turtle_right(angle)
turtle_forward(step)
cp <- round(turtle_getpos(), 0)
print(cp)
}
cat("All done!")
}Play the game a few times, to get a feel for how it works:
turtle_bounce(60, 15)Let’s examine the code a bit more closely.
The definition indicates that there are two parameters: side and step.
- The
sideparameter gives the dimensions of the Turtle’s field. Thus ifsidewere set to 60—which is the default—then the field would be a 60-by-60 square, with the origin \((0,0)\) in at lower-left corner and the point \((60, 60)\) at the upper-right corner. When the turtle is initialized it will appear in the middle of the square, at the point \((30, 30)\). stepspecifies how many units the turtle will move at each step. In this analysis we will assume thatstepis set to 15.
Inside the function, we begin with a bit of input-validation:
if ( (side/2) %% step != 0 ) {
stop("Side-length divided by two must be a multiple of step.")
}Remember that the turtle will start at \((\texttt{side}/2, \texttt{side}/2)\) and will move step each time. If \(\texttt{side}/2\) is not evenly divisible by step then the turtle would be able to go from inside its field to outside in a single step. We don’t want that to happen so we stop the user if the remainder after dividing \(\texttt{side}/2\) by side is anything other than zero.
If the input is OK, then we set up a vector bounds that records the smallest and largest possible values for the \(x\) and \(y\) coordinates of the turtle:
bounds <- c(0, side)Next, we initialize the turtle in the middle of the field and record its initial position in the vector cp:
turtle_init(side, side, mode = "clip")
origin <- turtle_getpos()
cp <- turtle_getpos()(You can think of cp as short for: “current position”.)
Next, we enter a repeat-loop. Inside the loop we begin with:
move <- readline(prompt = "Go Again? (enter q to quit): ")
if ( move == "q") break
x <- cp["x"]
y <- cp["y"]We first asked the user if she wanted to quit. If she enters “q” then we’ll break out of the loop and end the scenario. If she enters anything else (including just pressing Enter) then we record the \(x\) and \(y\) coordinates of the turtle’s current position in the vectors x and y respectively.
Our next task is to determine how the turtle should move:
if (x %in% bounds | y %in% bounds) {
angle <- 180
} else {
angle <- sample(c(0, 90, 180, 270), 1)
}If the turtle is at a boundary (either x equal to 0 or 60 or y equal to 0 or 60) then we need to “bounce back”. This corresponds to making the turtle turn right by 180 degrees and then step. On the other hand if the turtle is not at a boundary then the direction of the turtle should be random, so we should have it turn right by either 0, 90, 180 or 270 degrees, with each possibility being equally likely. This is accomplished with the above call to the sample() function.
Having determined the amount by which to turn prior to the next step, we then have the turtle turn that amount and take the step:
turtle_right(angle)
turtle_forward(step)Finally, we set cp to the new position of the turtle, and print that position out to the console for the user to see:
cp <- round(turtle_getpos(), 0)
print(cp)Note that we rounded off the position to the nearest while number. This was done because the authors of the TurtleGraphics package use floating point arithmetic for their numerical operations, so sometimes the computed positions differ from whole numbers by a very tiny amount.
We then repeat the loop.
5.4.3 Uniform Random Numbers.
sample() picks an element from a finite population. Sometimes, though, we want R to give the impression that it has picked a real number at random out of a range of real numbers. This can be accomplished with the runif() function.
A call to runif() looks like this:
runif(n, min = 0, max = 1)The idea is that R will produce n real numbers that have the appearance of having been drawn randomly from the interval of real numbers whose lower and upper bounds are specified respectively by min and max.
Thus, to get 10 “random” numbers that all lie between 0 and 1, you can leave min and max at their defaults and ask for:
runif(10) [1] 0.646902839 0.394225758 0.618501814 0.476891136 0.136097186 0.067384386
[7] 0.129152617 0.393117930 0.002582699 0.6202059545.4.4 Pseudo-Randomness and Setting a Seed
It’s important to point out that R doesn’t generate truly random numbers.2 After all, R simply runs a computer which operates according to a set of completely-specified steps. Thus the random data generated by R and by other computer languages is often called pseudorandom. Although the functions for random-number generation have been carefully designed so as to follow many of the statistical laws we associate with randomness in nature, all of the pseudo-random output is determined by an initial value and a deterministic number-generating algorithm.
We actually have the ability to set the pseudorandom data ourselves. This is called setting the random seed. From any specified seed, the result of calls to R’s random-data functions will be completely determined (although—just as in the case of “real” randomness—the output will still probably “look” random).
The set.seed() function will fix the random output. Try running the following two lines of code more than once:
set.seed(2025)
runif(10) [1] 0.7326202 0.4757614 0.5142159 0.4984323 0.7802845 0.5042522 0.8984003
[8] 0.1278527 0.6446721 0.5695311You will get the same output every time. If you change the argument of set.seed() to some other integer the output will probably change—but it will stay the same when you run the code again from that that new seed.
5.4.5 Application: a Drunken Turtle
We will now modify the previous scenario so that the turtle’s motion will be almost completely random. Even though it will take the same-size step every time, the angle at which it steps will be completely random: any real number of degrees from 0 to 360. We will also show the user the position of the turtle at each step, and use the “distance formula” from high-school geometry to compute and display the current distance of the turtle from the place where it started.
turtle_drunk <- function(side, step) {
turtle_init(side, side, mode = "clip")
# save (side/2, side/2), the turtle's initial position:
initial <- turtle_getpos()
repeat {
move <- readline(prompt = "Go Again? (enter q to quit): ")
if ( move == "q") break
# pick a random angle to turn by:
angle <- runif(1, min = 0, max = 360)
turtle_left(angle)
turtle_forward(step)
# get new position, make it the current position:
cp <- turtle_getpos()
# print to console:
print(cp)
# determine distance from initial position (round to 3 decimals):
distance <- round(sqrt((cp[1] - initial[1])^2 + (cp[2] - initial[2])^2),3)
# prepare message to console,and print it:
message <- paste0("Distance from starting point is: ", distance)
cat(message)
}
cat("All done!")
}Try the game once or twice:
turtle_drunk(100, 5)It is natural to wonder how likely the turtle is to wander back close to where it started, and to wonder how often that will happen. We will address questions like these in Chapter 6.
5.4.6 Practice Exercises
Many of these exercises don’t deal directly with turtles, but instead drill you on the sample() and runif()` functions.
For the next problem you should work in R Studio.
5.5 More Complex Turtle Graphs
Simple instructions, when combined with looping, can produce quite complex patterns. Consider the following process (with results shown in Figure 5.12):
turtle_init(1000, 1000, mode = "clip")
turtle_do({
turtle_setpos(600,400)
turtle_right(90)
for (i in 1:2000) {
turtle_right(i)
turtle_forward(sqrt(i))
}
})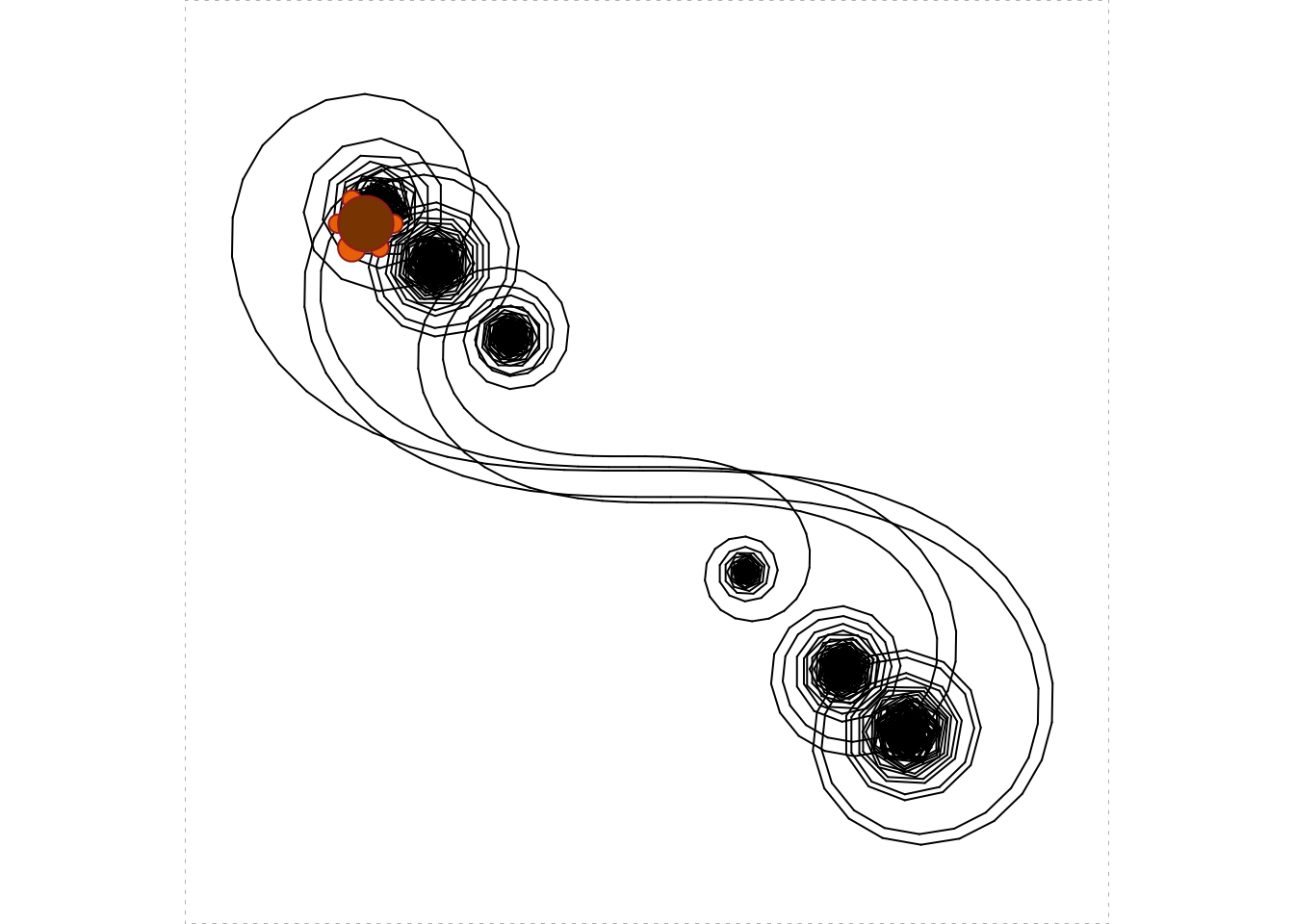
You might enjoy figuring out why this pattern occurs. As you ponder this, it might help to construct a set of “ragged” spirals with somewhat larger steps, and pause at each step. Code like the following might be useful:3
turtle_init(1000, 1000, mode = "clip")
turtle_do({
i <- 1
turtle_right(90)
repeat {
bidding <- readline("Proceed? (Enter q to quit) ")
if ( bidding == "q") break
turtle_right(i)
turtle_forward(2*sqrt(i))
cat(paste0("Turned ", i, " degrees,\n"))
cat(paste0("stepped forward ", round(2*sqrt(i), 3), " units.\n"))
cat("Turtle's current angle is: ", turtle_getangle(), " degrees.\n")
i <- i + 20
}
cat("All done!")
})5.6 Artistic Turtles
In Practice 5.11 you met the colors() function. Let’s have the Turtle put it to good use.
First of all, we might ask the Turtle to show us a sample of a given color:
turtle_show_color <- function(color) {
cat("I'm drawing a ", color, " square!", sep = "")
turtle_init()
turtle_col(color)
turtle_lwd(50)
turtle_do({
turtle_setpos(x = 30, y = 30)
turtle_square(40)
})
}Note the very thick lines specified above: turtle_lwd(50). Our turtle will draw a square with very thick sides that have the desired color. Let’s ask for burlywood. The resulting color-swatch is shown in Figure 5.13.
turtle_show_color("burlywood")
Feel free to ask for a random color. The result of the call below is shown in Figure 5.14.
turtle_show_color(sample(colors(), size = 1))
The function below is the Turtle’s attempt to dash off a quick imitation of the work of Jackson Pollack, the great American abstract expressionist:
turtle_quick_pollack <- function(strokes) {
turtle_init(mode = "clip")
turtle_lwd(50)
colorsUsed <- character(strokes)
turtle_do({
for ( i in 1:strokes ) {
randomColor <- sample(colors(), size = 1)
turtle_col(randomColor)
colorsUsed[i] <- randomColor
randomAngle <- runif(1, min = 0, max = 360)
turtle_left(randomAngle)
turtle_forward(10)
}
})
cat("Behold my masterpiece! It was painted with:\n")
print(colorsUsed)
}Note that the colors used are output to the console. Let’s have it make a picture with 50 strokes made by random-colored brushes. The resulting painting appears as Figure 5.15.
turtle_quick_pollack(50)Behold my masterpiece! It was painted with:
[1] "lightskyblue3" "gray12" "grey62" "cyan"
[5] "gray77" "lightpink3" "sandybrown" "gray57"
[9] "darkolivegreen2" "snow3" "grey43" "sandybrown"
[13] "grey79" "orangered1" "blanchedalmond" "gray95"
[17] "mediumpurple2" "darkgoldenrod4" "purple" "dodgerblue2"
[21] "grey93" "violetred" "steelblue2" "grey71"
[25] "gold4" "grey64" "goldenrod2" "brown3"
[29] "orangered2" "gray" "gray52" "darkgoldenrod3"
[33] "grey70" "lightslategrey" "aquamarine4" "grey71"
[37] "grey5" "darkslategray" "gray19" "ivory1"
[41] "deeppink" "mediumorchid" "palevioletred1" "wheat2"
[45] "tan" "springgreen" "thistle" "chartreuse3"
[49] "grey9" "royalblue4" 
5.7 Main Ideas of This Chapter
- For the most part Turtle Graphics are just a way for you to practice flow-control in an interesting setting. So as you review, put most of the emnphasis on the flow-control basics:
readline()for prompting;ifstatements andif-elsestatements;for-loops andwhile-loops.
- Random movement was one way of having fun with the Turtle, but randomization also really useful going forward, so really pay attention to the use you made of:
sample(), especially the new parameterprobthat lets you specify the probability of getting each of the elements of the vector you are sampling from;runif(), that lets you pick a real number that is equally likely to be anywhere between a specifiedminand a specifiedmaxvalue.
- Calling
set.seed()before you do randomization guarantees that you will get the same (but still random-looking) results every time you run your code. - When you do return to Turtle Graphics in the future, remember that you can make turtle-motions go faster by wrapping them in
turtle_do().
Glossary
- Pseudo-random Numbers
-
A sequence of numbers generated by a computer procedure designed to make the sequence appear to follow statistical laws associated with random processes in nature.
Exercises

Exercise 1
Write a function called turtle_gon() that draws a regular polygon. The user should be able to specify the side-length and the number of sides, so the function should take two parameters:
nfor the number of sides, andsidefor the length of the sides.
Start with a call to turtle_init() and test your function by drawing a regular dodecagon (twelve sides) with each side having a side length of 15 units, and, in a different place, a square having a side-length of 20 units. In your test the figures should not stray outside of the turtle’s field, so you may have to adjust the position of your turtle prior to each call to the function.
A typical test might go like this:
turtle_init()
turtle_setpos(x = 30, y = 50)
turtle_gon(n = 12, side = 15)
turtle_setpos(x = 10, y = 10)
turtle_gon(n = 4, side = 20)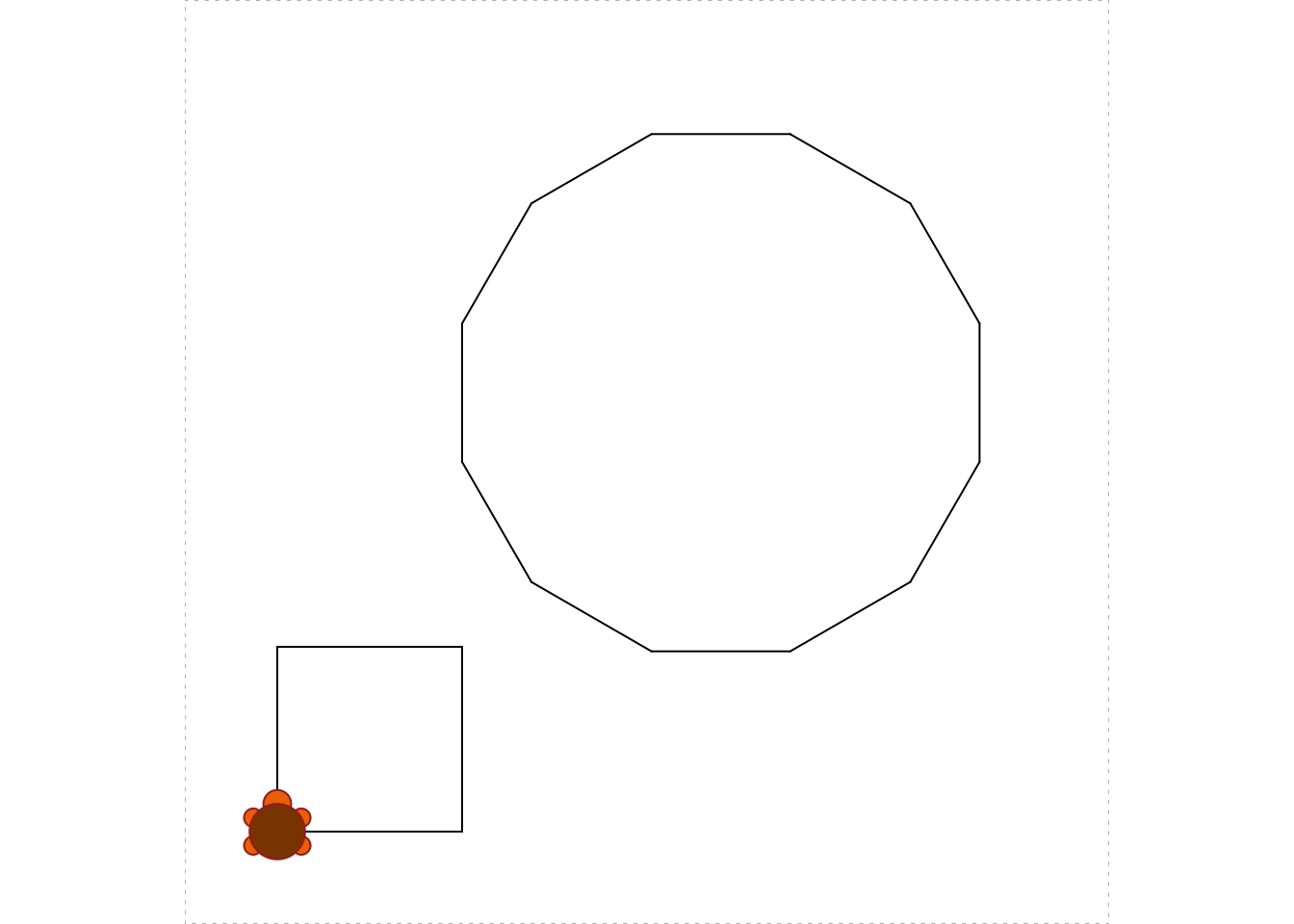
Notes and Hints: Within the function you should use a loop to make the polygon. The number of sides n is set by the user, so you’ll have to figure out for yourself how to compute the turning-angle after making a side. (Reviewing Practice 5.1 and Practice 5.2 should give you an idea for an expression for the turning-angle.) It is important to wrap your loop in a call to turtle_do(), as in the examples in this chapter, so the function will run quickly even when drawing polygons that have a lot of sides.
Exercise 2
Write a function called turtle_star() that can make stars like the ones in Figure 5.16.
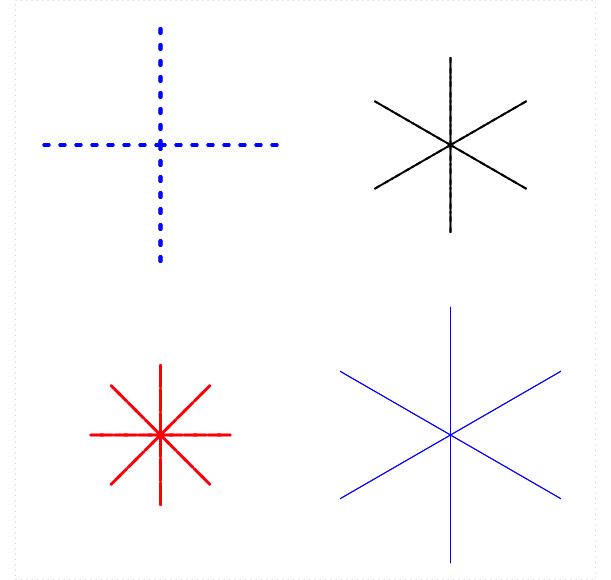
Here are the required parameters:
n: the number of rays in a star (default should be 6);length: the length of the rays (default should be 20);color: the color of the rays (default should be"red");type: the line-type of the rays (default should be 1);width: the line-width of the rays (default should be 1).
Unlike the previous exercise, the body of your function should include the call turtle_init(mode = "clip"), so that a new field is created when the function is run and there is no error if the user asks for a star that extends outside the field.
Among the test for your function, include one that creates a star with 10 rays, each of length 20 units. The lines should be red and dashed. I’ll leave the thickness up to you.
Hint: For a reminder on making stars, review some of the practice exercises in this Chapter.
Exercise 3
Modify the function from the previous exerise to make a new star-function called turtle_rstar(), in which the lengths of the rays are not determined by the user but instead vary randomly from 5 to 25 units, as in Figure 5.17:
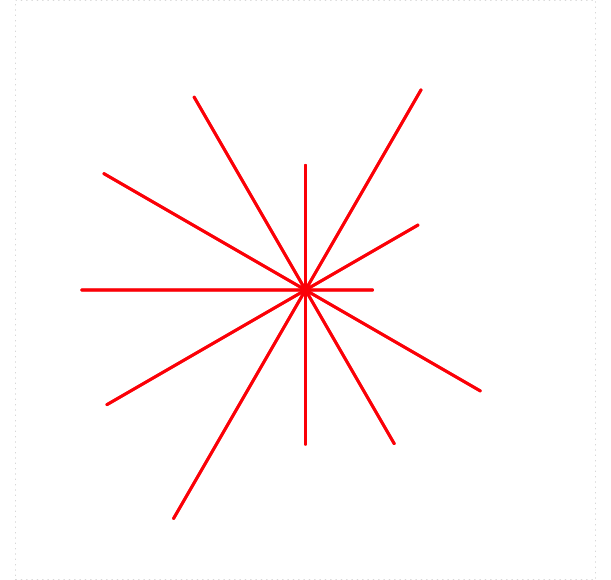
There is no longer a length parameter, but the names and default-values for the other parameters should be the same as in the previous exercise. In addition, the function should print out a report of the lengths of the rays, and a statment of the mean of these lengths.
Among the tests of the function, include one that makes a random star with 20 rays and a line-thickness of 3. (Other parameters should be left at their default-values.)
So for example, if you were to do the test described above, you would get results like this:
turtle_rstar(n = 20, width = 3)
The mean length was 16.95319.
The lengths themselves were:
[1] 7.219013 12.836147 24.502652 21.091332 15.580335 22.095631 9.620843
[8] 13.824802 7.730165 22.322622 10.535160 15.569156 19.246675 20.293817
[15] 21.096107 20.848620 12.000392 24.164186 23.715376 14.770812As in the previous exercise, please wrap your loop in a call to turtle_do().
Hint: To get each ray to have its own random length, review Practice 5.17. As for storing the lengths to report them at the end, review storage of colors in the Turtle Quick-Pollack function (see Listing 5.1).
Exercise 4
Make a new star function turtle_rstarColors() that behaves like turtle_rstar() except that instead of being determined by the user the ray-color varies randomly from one ray to another, as in Figure 5.18:
Each ray should have a color drawn randomly from the vector of all colors given by colors().
The function should also report the colors used to make the rays of the star.
Among the tests of your function, include one that makes a random star with 20 rays and a line-thickness of 6. Other parameters should be left at their default-values.
For example, if you were to test the function as described above, the results woud be like this:
turtle_rstarColors(n = 20, width = 6)
Colors of the rays were:
[1] "grey5" "gray54" "magenta4" "grey68"
[5] "darkslateblue" "limegreen" "grey62" "violetred2"
[9] "dimgrey" "navajowhite2" "dimgrey" "beige"
[13] "lightblue2" "darkorange1" "maroon1" "seashell"
[17] "turquoise3" "grey37" "coral" "lightskyblue" Hint: You’ll use a loop to draw the rays of the star. Within the loop you need to set the color of the ray you will draw. Practice 5.11 should remind you of a way to do this.
Exercise 5*
Our turtle_quick_pollack() function (see Listing 5.1) has successive strokes attached to each other. However, Jackson Pollack’s famous “drip” style involved placing brush-strokes at seemingly random locations on the canvas—successive strokes weren’t placed together. Modify our Pollack-painter function so that each new stroke appears as a random location inside the canvas. If you really get into it, research colors in R and try to come up with your own scheme for randomizing colors.
Turtle Graphics itself is not original to R. It was developed in the 1960’s by Seymour Papert for use in the LOGO programming language. LOGO is a general-purpose programming language but has been primarily used to teach programming concepts to children. Nevertheless, grown-ups enjoy playing with Turtle Graphics so much that implementations of the system are now found in several major “professional-grade” programming languages. For more information about Turtle Graphics, consult Papert (1993).↩︎
Indeed, philosophers of mathematics debate what randomness “really” is.↩︎
Also don’t forget that every 360 degrees is a full turn around the circle, so when the turtle’s angle is, say 720 degrees, it’s the same as an angle of 360 degrees which is the same as an angle of 0 degrees. All three angles amount to the same direction.↩︎