Elementary Statistics with R
Rebekah Robinson and Homer White
2016-06-15
Chapter 1 Introduction
1.1 What are R and RStudio?
R is a computer program that can do anything from basic arithmetic to complicated statistical analysis and graphs. Learning the language will take some time, but the best way to learn how to use R is by using it. So, let’s get started.
RStudio is an integrated development environment (IDE) that facilitates the use of R. In short, RStudio makes using R easier and more fun! You’ll notice that you have four panels in the RStudio window.
1.1.1 Panels and Tabs
The top left panel is called the Source. You will primarily be working with RScript (.R) and RMarkdown (.Rmd) files. To create a new file, select File, then New File, then select what type of file you want. This will open a new file with a template document to help you get started.
The bottom left panel is called the Console. This panel is the ‘brain’ of RStudio. Anything entered in this panel will be executed by R. Also, R only ‘knows’ what is entered into the Console.
The top right panel has two tabs - Environment and History. As commands are entered into the Console, they are simultaneously stored in the History tab. This gives you a running history of the work you do. You can Search through the History to locate previous commands. You can also highlight a previous command and send it back To Console or To Source. The Workspace tab shows the objects that the Console ‘knows’ - datasets, functions, etc.
The bottom right panel has four tabs that we will work with in this class - Files, Plots, Packages, and Help. The Files tab is exactly what it sounds like - it shows you a list of your available files and allows you to upload new files. The Plots tab displays the plots that you create in the Console. The Packages tab allows you to install and load necessary packages. The Help tab is where you will view R help files.
This will all start to make more sense as we go along, so don’t worry if it seems overwhelming at first. This information will be more useful as a reference tool as you start getting used to RStudio.
1.1.2 Differences Between RScript and RMarkdown Files
These descriptions of different types of files is not intended to overwhelm you on the first day of class! It should be treated as a resource for you to use as different points throughout the semester as you get used to using RStudio.
The most basic way to get RStudio to perform a command is to type the command directly into the Console. This tells R what you want it to do and it does it. The drawback to this is that you do not have a saved, and editable, copy of your commands. (Everything you type into the Console is automatically saved in the History tab. However, you cannot edit commands in the History tab.) This becomes an inconvenience if you are typing long commands. It is advantageous to store all of your commands in a file called an RScript. This way, you can go back and edit as you please. Once a command is typed into an RScript you can run it through the console a couple of different ways:
- You can select the entire command with your mouse. Then copy and paste it into the console.
- You can place your cursor on the line that contains your command and press the
Runbutton at the top right of the Source window.
Another type of file that you will use in this class is an RMarkdown file. It differs slightly from an RScript file. While it is likely that you will primarily read your course notes from the printed version you purchased from the bookstore, you will also have access to the RMarkdown version of these notes and your homework assignments. Other occasions will also arise throughout the semester where you will need to create RMarkdown documents.
RMarkdown documents integrate text with code into one document that can be compiled, or knit, into a readable HTML. The code in an RMarkdown document is offset by a ‘chunk’. This way, when you knit your HTML, the chunks will all be run through the console as Rcode and any output will be put in your HTML file.
While you are working in your RMarkdown document, you can run the code in a chunk several different ways:
- You can use your cursor and mouse to copy the code and paste it in the console.
- You can place your cursor anywhere in the chunk and select the ‘Run Current Chunk’ option in the ‘Chunks’ dropdown button at the top right of this window.
- You can place your cursor on the line you want to run and hit ‘Run’ at the top right of this window.
1.1.3 Basic R
In this class, anytime we use R, we will always start by loading two necessary packages.
The package tigerstats is the main package for our class. It includes all of the datasets, functions, and interactive apps that we will use throughout the semester. Anytime you do any work in RStudio for this class, you will want to require(tigerstats).
The mosaic package is a package that contains functions that we will use for some of our work this semester. For this reason, anytime you do any work in RStudio, you will also want to require(mosaic).
You will encounter various apps throughout this class that are designed to let you interactively explore concepts that we will be discussing in class. You should always take the time to tinker with these apps, as they will improve your understanding of difficult concepts. The package that must be loaded before you can use these apps is the package manipulate. Anytime you want to play with one of the apps in tigerstats, you must require(manipulate).
Let’s start by loading the necessary packages.
require(tigerstats)
require(mosaic)
require(manipulate) #if you want to play with an app in tigerstatsNote: Sometimes when you’re typing code into either a RScript or an RMarkdown, it’s nice to add a note to remind yourself what that particular line does. Anything that is typed after a # will not be run as Rcode in the console. It’s simply a note for yourself.
There are lots of cool features of R, but let’s begin by using R in the most basic way - like a calculator to do simple calculations.
5+4## [1] 924*3.7## [1] 88.818/3## [1] 6sqrt(81) #square root function.## [1] 9It’s that easy! R will do any arithmetic that you want. Just remember to use parentheses where they are appropriate to preserve order of operations.
1.1.3.1 Help
Now, suppose that you did not know what the command sqrt() did. You could get the help file for this command by typing help(sqrt) into the Console.
The Help tab will pop up and display the R Documentation for this command. It will give you:
- a description of what the command does,
- how it is entered into the Console,
- the arguments the command takes,
- some other details and references, and
- most importantly, examples of how to use it
Shortcut Help: If you type in the first couple letters of a command into the Console and then hit the Tab key on your keyboard, a Help window will pop up with possible matches and allow you to select exactly which one you want. If you still need more information, you can then hit F1 on your keyboard to open the Help tab to read more about it.
1.1.3.2 Assigning Values
If you want to assign a value to a place, you use the <- sign. For example,
mysum <- 5+6 This computes the value of 5+6 and assigns it to the object named mysum. This will not show you what the value is; it simply stores it. If you want to see the value of mysum, you need to call it by typing it into the console (or a code chunk in an RMarkdown file).
mysum ## [1] 11myproduct<-5*6
myproduct## [1] 30Assigning values to an object allows you to access them later by their name. For example, suppose that I wanted to add 10 to whatever value I had stored in mysum earlier in my work.
mynewsum <- mysum+10
mynewsum## [1] 21Notice that you can choose any name that you wish for the object (the name to the left of the <-). However, you must be careful with what you type to the right of the <-. This must be recognizable by R. It should either by a number, a function, or an object that you have already assigned a value to.
While it does not really matter what you choose to name objects, you should be a little bit careful.
- It is helpful to choose a name that is descriptive. Notice that we chose the name
mysumandmynewsumfor the sums that we computed above.
- You do not want to name an object something that is already used as a function name or the name of a dataset. This is both confusing and can cause problems for you later.
- You can use some symbols in your names, such as a period (.) and an underscore (_). However, you cannot include other symbols or spaces in your object names.
1.1.3.3 Several Important Functions
1.1.3.3.1 Concatenation Function
Let’s talk about a function that you will see and use alot this semester. The concatenation, c() function combines values into a list. Creating a list of the numbers 1, 3, and 5 can be accomplished by:
mylist <- c(1,3,5)
mylist## [1] 1 3 5If you want to combine letters (or words), you must put them in quotes. You can remember this by thinking of R as a really fancy calculator. R operates with numbers and functions, so letters and words have to be treated differently by placing them in quotes.
mygrades <- c("A", "B", "C", "D", "F")
mygrades## [1] "A" "B" "C" "D" "F"1.1.3.3.2 Replicate Function
Suppose we want to create a list of numbers that are all the same. For example, say we want to make the list 1,1,1,1,1. We could accomplish this with the concatenation function by
myreps <- c(1,1,1,1,1)
myreps## [1] 1 1 1 1 1This will work, but there is an easier way to do this, using the replicate function, rep().
myreps <- rep(1,5)
myreps## [1] 1 1 1 1 1The replication function requires two inputs. The first input is the value that we want to be replicated and the second is the number of times we want that value replicated.
You can also combine the concatenation and replication functions to create a list of repeated letters or words. Just make sure that you use quotes for the letters.
myletters<-c(rep("A",3),rep("B",10),rep("C",7))
myletters## [1] "A" "A" "A" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "C" "C" "C" "C"
## [18] "C" "C" "C"1.1.3.3.3 Sequence Function
Suppose we want to create a list of numbers that appear in a certain sequence. For example, say we want to make the list 1, 2, 3, 4, 5, 6. Again, we could accomplish this with the concatenation function.
myseq <- c(1,2,3,4,5)
myseq## [1] 1 2 3 4 5The sequence function, seq(), makes this task easier.
myseq <- seq(from=1, to=5, by=1)
myseq## [1] 1 2 3 4 5The sequence function requires three pieces of information.
* Where the sequence should start, from= * Where the sequence should end, to= * The increment, by=
Suppose we want to create the sequence 55, 57, 59, 61, 63, 65, 67, 69, 71.
seq(from=55, to=71, by=2)## [1] 55 57 59 61 63 65 67 69 71Notice that we did not store the sequence above in a object. The sequence was still created, but we will not be able to access it later.
That should be enough to get you started (and overwhelmed). Remember, treat this chapter as a reference guide to help you throughout the semester.
1.2 Let’s play cards!
1.2.1 The Game
We are going to introduce an important statistical concept that will be a continuing theme throughout this class by playing a game with a standard deck of cards. In a standard 52 card deck, there are 4 suits (Hearts, Diamonds, Spades, Clubs). Each suit has an Ace, King, Queen, Jack, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Half of the cards are red (Hearts and Diamonds) and half of the cards are black (Spades and Clubs).
Here’s the game: A volunteer draws 10 cards from our classroom deck of cards, with replacement. The cards will be shuffled between each draw. The volunteer wins a point for each red card drawn and the dealer wins a point for each black card drawn.
Drawing the cards with replacement means that the volunteer will draw one card, record the color, and then put it back in the deck before drawing another card. Doing it this way assures that each color has the same chance of being drawn each time.
Let’s think about a couple of questions before playing. If we are playing with a standard deck,
What is the probability that the volunteer will pull out a red card?
Of the 10 cards drawn, how many do you expect to be red?
This is our best guess (hypothesis), based on the information we have at hand.
- Do we think that the volunteer will draw exactly the hypothesized number of red cards?
There is randomness at play when we draw cards from a deck.
Okay, enough thinking. Let’s play!
1.2.2 The Results
Suppose that our class drew 9 red cards (out of 10 cards drawn). Consider the following questions:
Do these results seem consistent with how many we expected to be red? Or do they seem strange?
Do you still believe your hypothesized probability of drawing a red card? In other words, do you still believe that we are playing with a standard deck?
Although these results may seem strange, this was only one game. We agreed that there is randomness at play here, so our results may have just been a fluke. Let’s test this by playing the game again. Better yet, we can speed things up by simulating the game in RStudio. This way, we can play lots of games quickly to see if the results we got in our classroom game are really that surprising.
We can easily create a virtual deck of cards using the concatenation function. Since we only care about the color of the card (not the suit or the face value), let’s make it easier to count by using a virtual deck that tells us only the color. We’ll need 26 red cards and 26 black cards.
mycards<-c(rep("Red",26),rep("Black",26))
mycards## [1] "Red" "Red" "Red" "Red" "Red" "Red" "Red" "Red"
## [9] "Red" "Red" "Red" "Red" "Red" "Red" "Red" "Red"
## [17] "Red" "Red" "Red" "Red" "Red" "Red" "Red" "Red"
## [25] "Red" "Red" "Black" "Black" "Black" "Black" "Black" "Black"
## [33] "Black" "Black" "Black" "Black" "Black" "Black" "Black" "Black"
## [41] "Black" "Black" "Black" "Black" "Black" "Black" "Black" "Black"
## [49] "Black" "Black" "Black" "Black"Let’s again start by shuffling the deck.
shuffle(mycards)## [1] "Black" "Black" "Red" "Red" "Black" "Red" "Black" "Black"
## [9] "Black" "Red" "Red" "Red" "Black" "Red" "Red" "Red"
## [17] "Black" "Red" "Red" "Red" "Black" "Red" "Red" "Red"
## [25] "Red" "Red" "Red" "Red" "Red" "Black" "Red" "Black"
## [33] "Black" "Black" "Black" "Black" "Red" "Black" "Red" "Black"
## [41] "Black" "Black" "Black" "Black" "Red" "Red" "Black" "Black"
## [49] "Black" "Black" "Black" "Red"We will randomly deal 10 cards from this new deck using the sample function. The sample function takes three arguments. You need to tell is where to sample from, how many to sample, and whether or not to sample with replacement.
sample(mycards, size=10, replace=TRUE)## [1] "Black" "Red" "Red" "Red" "Black" "Black" "Red" "Red"
## [9] "Black" "Red"Let’s create a table to count the number of red cards and black cards that were in our hand of 10.
table(sample(mycards, size=10, replace=TRUE))##
## Black Red
## 4 6Again, this was just one game. We would like to repeat this lots of times to see if our class results were really that unusual. We are looking to answer the questions:
- How often do we see our in-class results when we’re playing with a standard deck? * What are the chances (or probability) of seeing our in-class results when we’re playing with a standard deck?
Let’s repeat the game three times.
do(3)*table(sample(mycards, size=10, replace=TRUE))## Black Red
## 1 7 3
## 2 4 6
## 3 2 8The first row of this table represents the first game in which 7 black cards were drawn and 3 red cards were drawn. The second row of this table represents the second game in which 4 black cards were drawn and 6 red cards were drawn. The third row of this table represents the third game in which 2 black cards were drawn and 8 red cards were drawn. If you wanted to simulate more games, you could change the 3 in the line of code above. For example, suppose you wanted to simulate 20 games. You would simply type:
do(20)*table(sample(mycards, size=10, replace=TRUE))Let’s look at this another way by creating a table that keeps track of how many of our games result in a certain number of red cards drawn.
## Red
## 0 1 2 3 4 5 6 7 8 9 10
## 0 0 0 1 0 0 1 0 1 0 0The first row of this table represents the number of red cards drawn. The second row gives the number of games (out of the three that we played) that resulted in drawing that many red cards. We had one game where 3 red cards were drawn, one game where 6 red cards were drawn, and one game where 8 red cards were drawn.
We could get an even better idea of what’s going on if we could simulate the game many times, say 1000 times! We will create the same type of table we just did to keep track of these games.
## Red
## 0 1 2 3 4 5 6 7 8 9 10
## 0 5 41 119 205 249 209 121 42 8 1At this point, it’s starting to seem that drawing a high number of red cards doesn’t happen very often. It seems unlikely, but it sure would be nice to have an idea of just how unlikely it is.
Perhaps having this table in terms of percents is more useful:
##
## Red 0 1 2 3 4 5 6 7 8 9 10 Total
## 0 0.5 4.1 11.9 20.5 24.9 20.9 12.1 4.2 0.8 0.1 100Consider the following questions based on our simulation:
If we draw 10 cards from a standard deck,
- What is the estimated chance of drawing 5 red cards?
Answer: There is a 24.9% chance of drawing 5 red cards.
- What is the estimated probability of drawing 1 red card?
Answer: There is a 0.5% probability of drawing 1 red card.
- How likely is it that our volunteer drew their original hand, based on our simulations?
Answer: Assuming that our volunteer drew 9 red cards, the likelihood that our volunteer drew their original hand (based on our simulations) is 0.8%.
Based on this likelihood, does it seem reasonable to believe that the deck we used in class was a standard deck?
Let’s check out how RStudio can help us to visualize the data from our 1000 simulated games graphically, in the form of a histogram. We will be learning more about histograms in Chapter 2.
Here is the table again followed by the graphical representation (histogram). See Figure[Histogram].
##
## Red 0 1 2 3 4 5 6 7 8 9 10 Total
## 0 0.5 4.1 11.9 20.5 24.9 20.9 12.1 4.2 0.8 0.1 100## Warning in mean.default(eval(formula[[2]], data, .envir), ...): argument is
## not numeric or logical: returning NA## Warning in var(if (is.vector(x) || is.factor(x)) x else as.double(x), na.rm = na.rm): Calling var(x) on a factor x is deprecated and will become an error.
## Use something like 'all(duplicated(x)[-1L])' to test for a constant vector.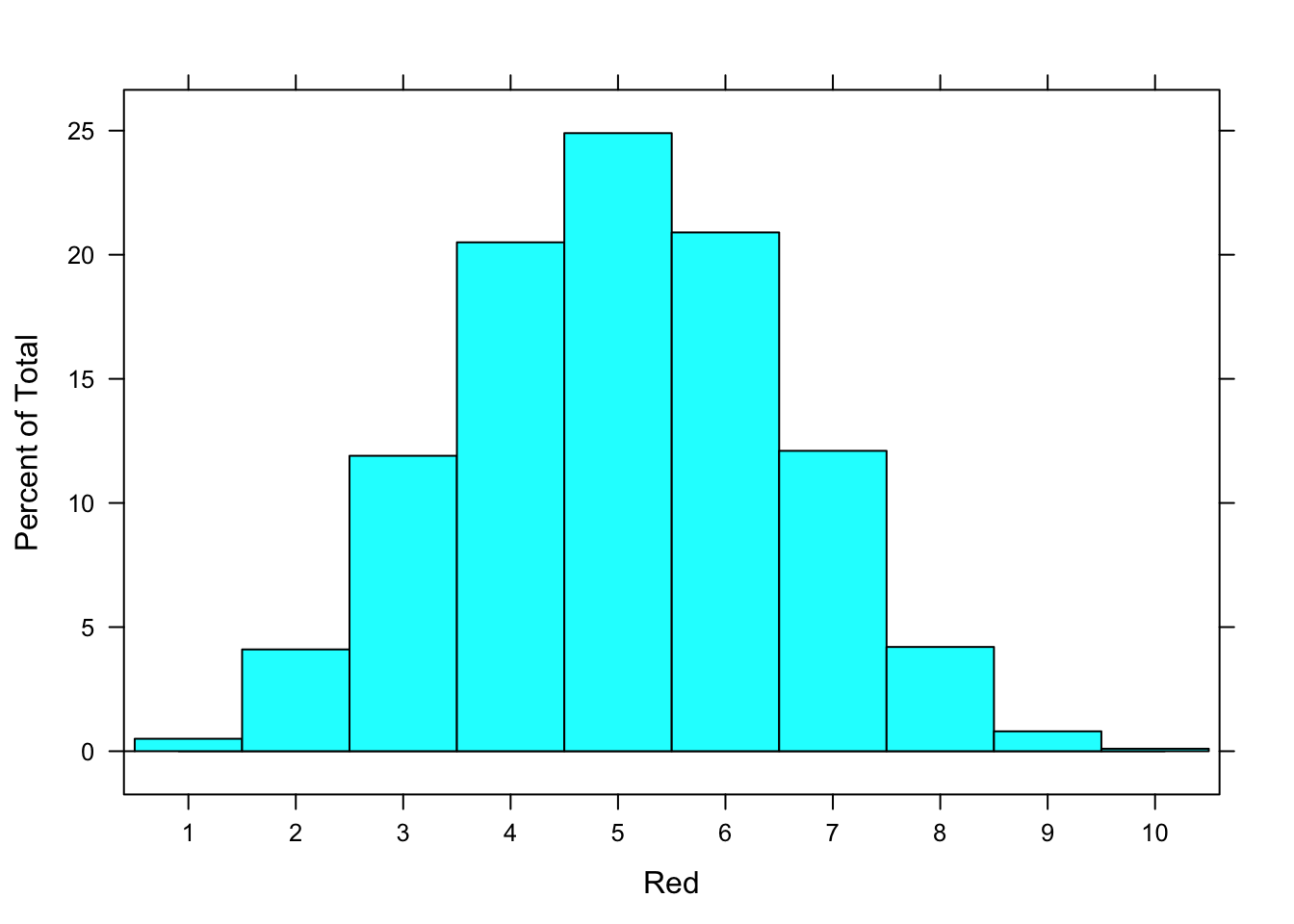
Figure 1.1: Histogram: Graphical representation of the table of counts for the 1000 simulated games.
The horizontal axis gives us the number of red cards drawn in a hand of 10 cards from a standard deck. The vertical axis gives us the percent of times (out of the 1000 simulated games) that a particular number of red cards was drawn.
Notice that the width of each bar in the histogram is 1 and the height of each bar is equal to the percent of the 1000 games that resulted in that number of red cards.
We can color the bar in the histogram to mark how many red cards our volunteer drew in the class game. See Figure[Class Probablity].
## Warning: 'perctable' is deprecated.
## Use 'tally' instead.
## See help("Deprecated")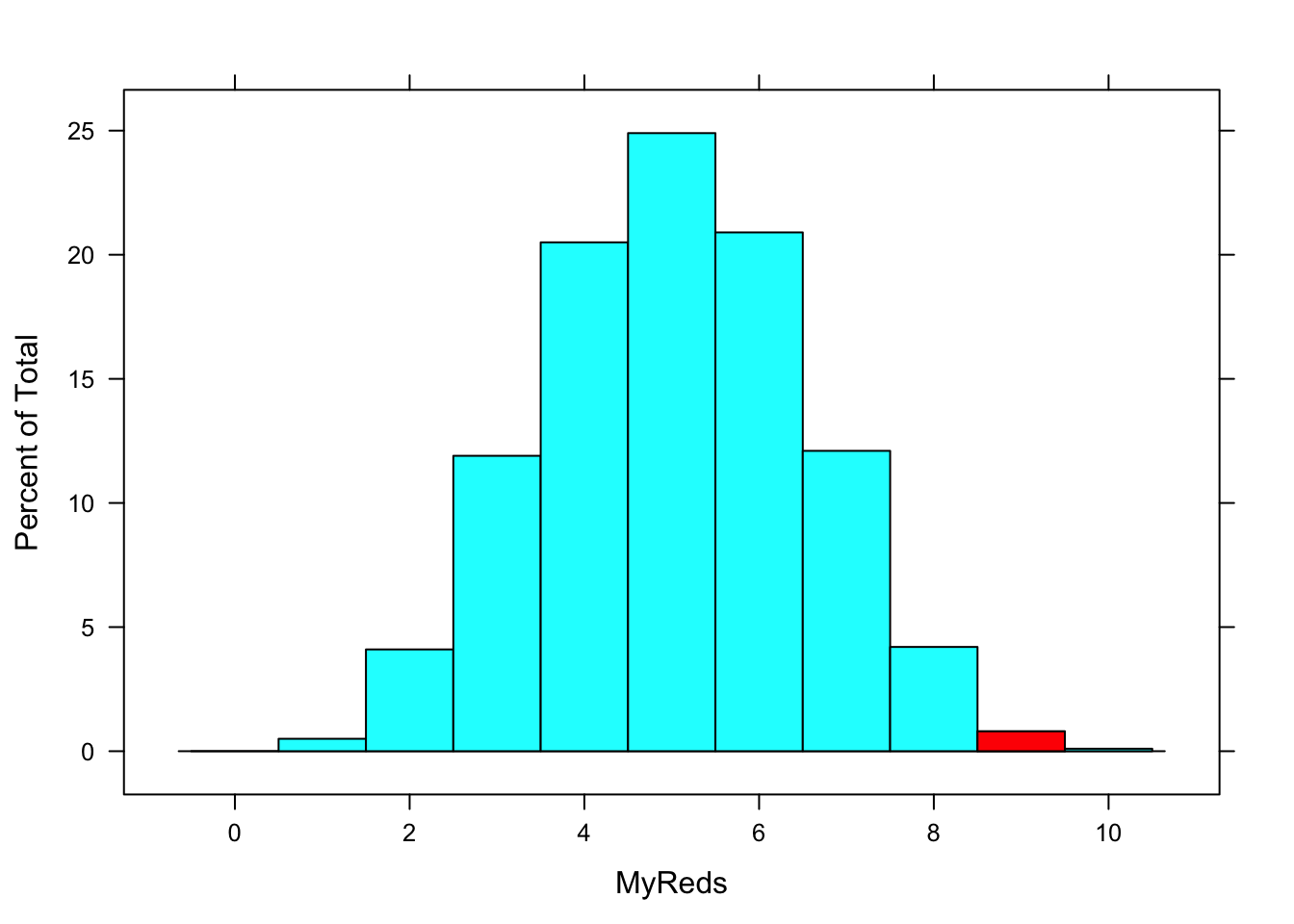
Figure 1.2: Class Probability: The shaded rectangle in the histogram represents the probability that the volunteer would draw 9 cards if they were drawing from a standard deck of playing cards.
This colored part of the histogram represents the estimated chance of drawing our particular draw from a standard deck.
We can think about how likely it is that our class game resulted in such a high number of red cards (or higher). This likelihood is called a p-value. We can compute the p-value numerically and view it graphically on the histogram.
Numerically, the p-value is:
## Warning: 'proptable' is deprecated.
## Use 'tally' instead.
## See help("Deprecated")## 9
## 0.009The p-value is the estimated probability of drawing as many red cards or more (out of 10) as our volunteer drew if we are drawing from a standard deck of playing cards.
Graphically, the P-value is the total area in the histogram that lies to the right of the vertical line in the graph. See Figure[P-Value].
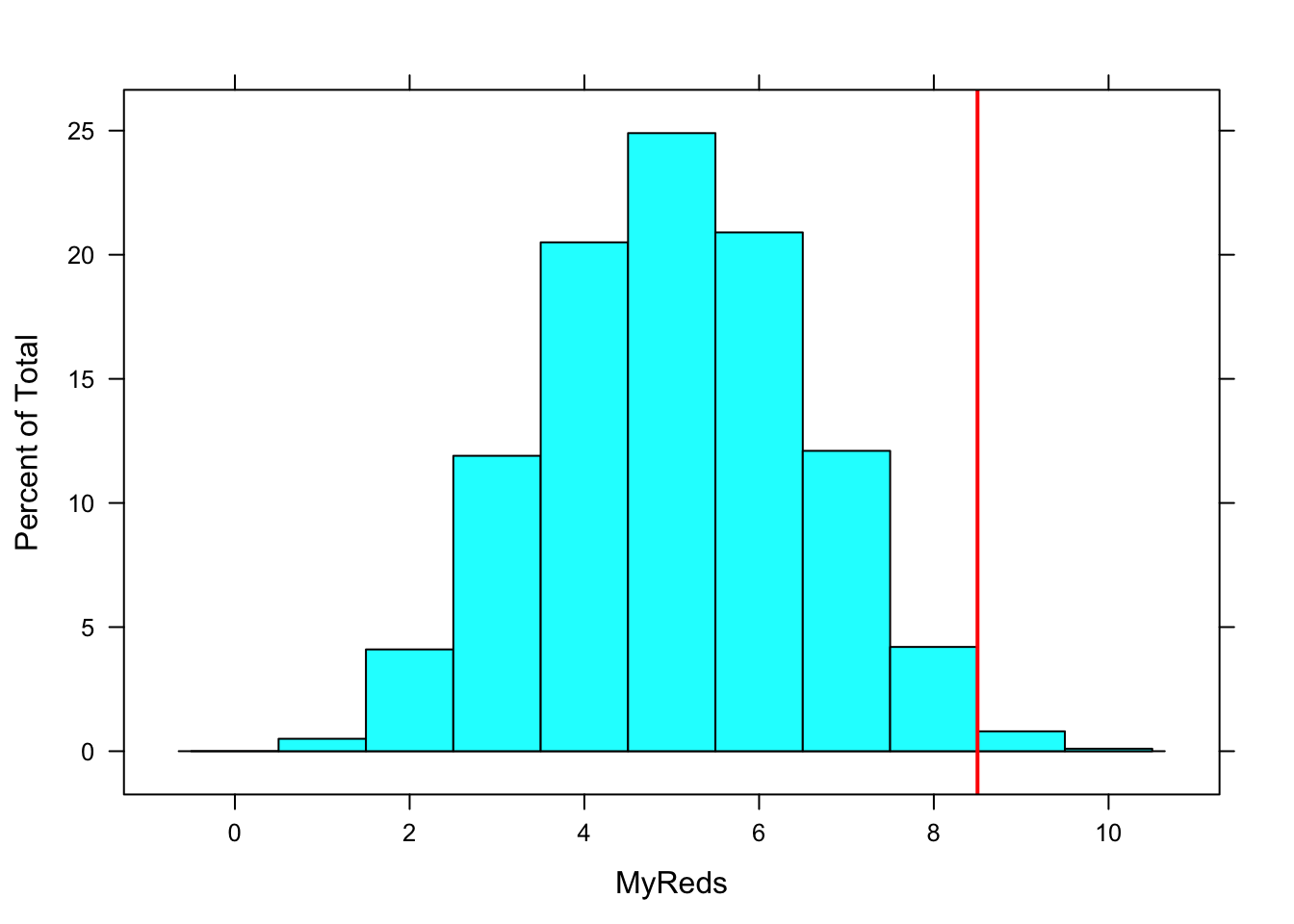
Figure 1.3: P-Value: The area of the histogram that lies to the right of the vertical line is the p-value.
1.2.3 The Conclusion
Summing this up:
We started with a hypothesis. We assumed that we were playing with a standard deck.
We gathered data from a real-world experiment to test our hypothesis. We played one real game.
Our results seemed strange, so we wondered if our hypothesis was true. We questioned: How likely was it to draw the hand that we did if we drew from a standard deck?
We tested the hypothesis by simulating 1000 games using R. We counted up the number of games that gave us the result we got in class.
We calculated a P-value, the probability of getting results as extreme as ours (or more so!) from a standard deck.
Finally, we need to draw a conclusion.
Conclusion: If we assume that our volunteer drew 10 cards from a standard deck of cards, there is about a 0.009 (0.9 %) chance of drawing 9 red cards. Since the probability of drawing 9 (or more) red cards is so small, this should cause you to question whether the volunteer was really drawing from a standard deck.
1.3 Statistics
The ultimate goal of statistics is to translate data into knowledge and understanding of the world around us. It’s the art and science of learning from data!
The card game we played above is a perfect example of the three aspects of statistics.
Design - asking the right questions and collecting useful data.
After we played the card game in class, we questioned whether we were playing with a standard deck of cards. We came up with a logical way to test whether our results were really as unlikely as they seemed. We used the power and speed of RStudio to quickly simulate 1000 games. This was our data.
Description - summarizing and analyzing data.
Once we had the raw data, we summarized it in the form of a table and a histogram. These summaries allowed us to analyze the data by calculating a p-value. A p-value is the probability of obtaining our results (or more extreme results) if our original hypothesis is true.
Inference - making decisions, generalizations, and turning data into new knowledge.
This is where the art of statistics comes into play. Based on your analysis, how convinced are you that the deck was stacked? How much evidence is enough? Were you convinced after 1 game, 3 games, 1000 games? Are you convinced now or do you think we should gather more data?
These are all ideas that we will investigate more thoroughly throughout the semester! As we continue to talk about these things, keep the Card Game in mind as a reference example.
1.4 Thoughts on R
Important R commands:
a+bbasic addition, “a plus b”a-bbasic subtraction, “a minus b”a*bbasic multiplication, “a times b”a/bbasic division, “a divided by b”
Know how to use these functions:
sqrt()square root functionhelp()help function will pull up the help file for any function for which you need more informationc()concatenation function combines values, letters, or words into a listrep()replication function creates a list of repeated values, letters, or words.seq()sequence function creates a sequence of values starting and ending at a specified spot with a specified increment.
Always remember to require() the needed packages.
require(tigerstats)anytime that you open a new Rscript or RMarkdown file.require(knitr)anytime that you are working in a RMarkdown file.
require(manipulate)anytime you want to run one of the class apps, available intigerstats.